LIGNES DE TRANSMISSION

LIGNES DE TRANSMISSION

On appelle ligne de transmission un ensemble de conducteurs cylindriques à génératrices parallèles qui assure le transport de l’énergie électrique entre deux points donnés. Les lignes de transmission présentent une diversité très grande selon les gammes de fréquence où elles sont utilisées. En électrotechnique, l’énergie électrique est véhiculée du lieu de production au lieu d’utilisation par des lignes à deux, trois ou quatre fils. Elles servent alors au transport de courants de très basses fréquences (continu, 50, 60 ou 400 Hz). En téléphonie, la correspondance entre abonnés est assurée soit par des lignes aériennes bifilaires, soit par des câbles coaxiaux sous-marins ou souterrains, soit par des ondes herztiennes, soit par des fibres optiques. En radiotechnique, pour relier l’antenne à l’émetteur ou au récepteur, on se sert également en général de lignes coaxiales.

Dans le domaine des hyperfréquences, l’onde électromagnétique peut se propager à l’intérieur d’un tuyau métallique creux appelé «guide d’onde», ou le long de câbles coaxiaux ou de «lignes à ruban triplaques» (stripline ); signalons enfin la technique de la ligne à ruban dite microstrip .

Ces différentes lignes de transmission possèdent un caractère commun: une de leurs dimensions géométriques est grande par rapport à la longueur d’onde et il n’est pas question, dans ces conditions, de leur appliquer l’approximation des états stationnaires.

Leur étude théorique est alors fondée sur les équations de Maxwell, auxquelles on ajoute les conditions aux limites imposées par les surfaces de séparation entre les milieux différents, ainsi que les relations particulières aux matériaux employés; les formes géométriques simples des lignes permettent en général des simplifications dans les calculs. Depuis la Seconde Guerre mondiale, les problèmes théoriques et techniques relatifs aux lignes de transmission sont bien connus; on assiste à un développement intensif des réalisations technologiques, en regard des besoins toujours croissants. On se limitera ici à présenter les aspects théoriques des lignes de transmission, renvoyant le lecteur à l’article MICROÉLECTRONIQUE pour les problèmes techniques.

1. Les équations de Maxwell dans les lignes de transmission

Les équations de Maxwell s’écrivent:

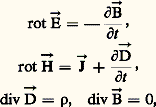où つ désigne le champ électrique, で le champ magnétique, っ l’induction électrique, ち l’induction magnétique, ど la densité de courant et 福 la densité des charges électriques (cf. ÉLECTRICITÉ - Électromagnétisme).

Quel que soit le milieu considéré, on peut toujours ramener le problème d’intégration de ces équations au cas où 福 = 0. En effet, pour un conducteur donné, la constante de temps de dissipation des charges électrostatiques est d’une durée très inférieure à la période du champ alternatif de l’onde; on peut donc considérer le conducteur comme un milieu continu et supposer 福 = 0. Dans le cas d’un diélectrique, le champ électrique peut être considéré comme la somme du champ électrostatique dû aux charges électriques invariantes et du champ qui constitue la solution des équations de Maxwell en milieu déchargé ( 福 = 0). On est ainsi en présence de phénomènes linéaires, donc superposables. En cherchant des solutions dont la dépendance du temps est de la forme e ^j size=1^諸t et en tenant compte des relations constitutives du milieu on obtient:

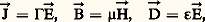où 臨 désigne la conductivité électrique, 猪 la perméabilité magnétique, et 﨎 la permittivité diélectrique.

On établit les équations qui régissent les champs, dites «équations des ondes »:

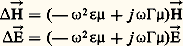à partir desquelles on obtient les constantes de propagation, les vitesses des propagations, le rapport des amplitudes des champs, les phases relatives des champs, d’où l’impédance d’onde et le rapport des énergies électriques et magnétiques.

Dans le cas de milieux finis, il faut de plus satisfaire aux conditions aux limites sur les surfaces de séparation des milieux 1 et 2: continuité de la composante normale des vecteurs inductions électrique et magnétique, continuité de la composante tangentielle des vecteurs champs électrique et magnétique.

Ondes planes

Dans le cas de milieux infinis, on est amené à chercher les solutions de la forme:

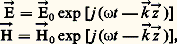où ん désigne la direction de propagation et や le vecteur d’onde.

Ces solutions correspondent à des ondes planes et vérifient donc les relations:

Dans les milieux conducteurs parfaits, les champs つ et で sont nuls. Dans les milieux diélectriques parfaits, les champs つ et で ne sont pas atténués, ils sont en phase et les énergies électriques et magnétiques sont égales. Dans les milieux bons conducteurs, les champs sont atténués suivant la loi exponentielle: exp (face=F0019 漣 z / 嗀), la profondeur de pénétration, appelée encore «épaisseur de peau», s’exprimant par:

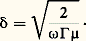Les champs y sont en quadrature et l’énergie se trouve essentiellement sous forme magnétique.

Ondes guidées

On recherche les solutions des équations de Maxwell dans les systèmes à symétries cylindriques, solutions appelées ondes guidées. On les trouve de la forme: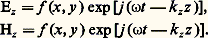

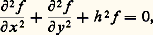La fonction f (x , y ) est solution d’une équation du type:

où h = constante. Il faut aussi adjoindre à ces solutions générales les conditions aux limites à l’interface.

On trouve deux types de solutions indépendantes:

– dans le cas des ondes TM (transverse magnétique), pour lesquelles H^z = 0, E^z = f , つ^xy est alors proportionnel à gradf , で^xy se déduit de つ^xy par rotation de + 神/2 avec un facteur de proportionnalité complexe;

– dans le cas des ondes TE (transverse électrique), pour lesquelles E^z = 0, H^z = f , で^xy est proportionnel à gradf , つ^xy se déduit de で^xy par rotation de 漣 神/2 avec un facteur de proportionnalité complexe.

Dans un guide à section rectangulaire ou circulaire, on trouve des solutions fonctions de deux paramètres entiers m , n (TE^mn ou TM^mn ), qui indiquent les variations des champs suivant les deux directions de la section du guide rectangulaire, ou suivant deux rayons du guide circulaire.

Dans tous les cas, il existe une fréquence dite de coupure, en deçà de laquelle il n’y a plus de propagation de l’onde suivant l’axe mais onde évanescente, donc atténuation. Dans le cas de milieu non parfait, il y a des pertes d’énergie dans le conducteur et un affaiblissement dans le diélectrique; on définit alors une constante d’affaiblissement.

2. Caractéristiques des ondes de propagation TEM le long d’une ligne de transmission

Champs électrique et magnétique

On est amené à trouver les équations des champs d’une onde susceptible de se propager le long d’une ligne de transmission ZZ avec une vitesse 轢v. On cherche des solutions de la forme:

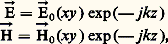avec, en outre, les conditions suivantes:

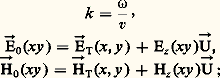où つ^T et で^T sont les composantes de つ et で suivant le plan de section ( ゑ, を).

Dans ces conditions, on montre, à l’aide des équations de Maxwell, que seules les composantes つ^T et で^T ne sont pas nulles (fig. 1).

On appelle cette onde: transversale électromagnétique, en abrégé TEM. Le champ électrique est défini par les équations:

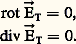Il dérive donc d’un potentiel V(xy ): face="EU Arrow" つ^T = 漣 gradV.

Le champ magnétique s’écrit alors:

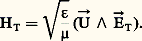Courants et tensions

Appelons i ^s la densité de courant superficielle le long de la ligne. En un point quelconque du conducteur où ょ est le vecteur unitaire de la demi-normale extérieure, le théorème d’Ampère permet d’écrire:

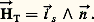Les lignes de courant sont donc constituées par les génératrices de la ligne de transmission (fig. 2). Le courant qui circule dans un conducteur se calcule directement à partir de l’expression de H^T et il se formule:

Appliquons ce qui précède au cas d’une ligne bifilaire ; on suppose, comme cela se produit toujours en dehors des ondes centimétriques, que la longueur d’onde du signal appliqué est très grande vis-à-vis de la distance des deux conducteurs. Le travail du champ électrique le long d’une trajectoire quelconque située dans leur plan de section droite et allant du conducteur 1 au conducteur 2 est indépendant du choix de cette trajectoire (fig. 3); il définit la différence de potentiel ou encore la tension entre les deux conducteurs: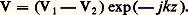

Impédance caractéristique et impédance de ligne

On appelle «impédance caractéristique» d’une ligne où se propage une onde progressive le rapport Z^c = V/I. Lorsque le mode de propagation est du type TEM, ce rapport est réel et indépendant du point choisi. Par exemple, pour une ligne bifilaire constituée par deux fils parallèles identiques de diamètre a , dont les axes sont distants de D:

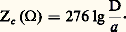Jusqu’à présent, nous avons considéré qu’il ne circulait qu’une seule onde progressive sur la ligne. Il peut arriver que deux ondes circulent en sens inverses. V¹ et V² étant leurs amplitudes respectives, les tensions transportées par chacune des ondes s’expriment, au point d’abscisse z :

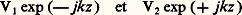et donnent naissance à une tension résultante:

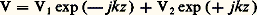et au courant résultant:

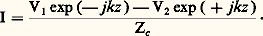On démontre alors qu’il existe sur la ligne une succession de points séparés par des intervalles égaux à la demi-longueur d’onde où la tension est maximale et égale à |V¹| + |V²|: ce sont les ventres de tension. Au milieu de deux maximums, la tension est minimale et égale à |V¹| 漣 |V²|: ce sont les nœuds de tension. Le courant possède lui aussi une succession de maximums et de minimums, un nœud de courant correspondant à un ventre de tension et inversement. On retrouve ainsi les caractéristiques générales de tous les phénomènes d’ondes stationnaires, et l’on appelle alors impédance de ligne le rapport, en un point quelconque:

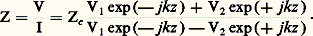Transformation d’impédance le long d’une ligne désadaptée

Une impédance Z^r , branchée à l’extrémité d’une ligne d’impédance caractéristique Z^c , provoque l’apparition d’un système d’ondes stationnaires.

En utilisant l’expression de l’impédance de ligne, nous pouvons en ce point écrire:

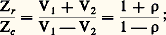le rapport 福, appelé «coefficient de réflexion», s’exprime:

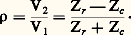En un point quelconque, l’impédance de ligne peut s’écrire:

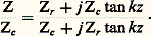Trois cas particuliers sont intéressants:

(a ) Z^r = Z^c ; 福 = 0 en tout point, Z = Z^c ; il n’y a pas d’onde réfléchie, on dit que la ligne est «fermée» sur son impédance caractéristique;

(b ) Z^r = 0; la ligne est fermée par un court-circuit et 福 = 漣 1, V² = 漣 V¹.

L’impédance de ligne au point d’abscisse z est Z = j tan kz ; la ligne se comporte comme une réactance pure, alternativement positive et négative; en particulier, aux points z = 神/2k =/4, cette réactance est infinie;

(c ) Z^r infinie; la ligne est dite «ouverte» et 福 = + 1, V² = V¹.

L’impédance de ligne en un point z quelconque est:

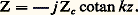On voit qu’il est possible d’utiliser les lignes comme éléments de liaison entre un générateur d’énergie et une impédance d’utilisation Z^r pour réaliser une transformation d’impédance et permettre ainsi l’adaptation de Z^r au générateur. On se sert alors d’abaque d’impédance réduite z = Z/Z^c . Le plus couramment utilisé est l’abaque de Smith.

Dans la pratique, on définit le coefficient:

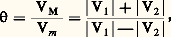appelé «taux d’ondes stationnaires» (en anglais, V.S.W.R. = Voltage Standing Wave Ratio). Il est, en effet, aisément mesurable: on déplace le long de la ligne de transmission un chariot muni d’une sonde exploratrice qui, placée dans la section droite de la ligne, est le siège d’une force électromotrice proportionnelle au champ électrique, donc à la tension V. Après détection, on peut ainsi, à l’aide d’un appareil de mesure à courant continu, mesurer |V| en valeur relative. Une exploration sur une longueur au moins égale à/2 permet de mesurer et d’en déduire le coefficient de réflexion en valeur absolue:

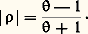Schéma équivalent à une ligne de transmission

Considérons un tronçon de ligne d’impédance caractéristique Z^c de longueur l , terminée par une impédance Z^r . On montre que son impédance d’entrée Z¹, peut s’écrire:

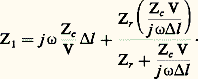On pose:

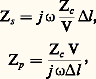et le tronçon de ligne l est équivalent au schéma indiqué figure 4.

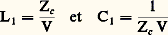sont appelés respectivement inductance et capacité par unité de longueur. L’impédance caractéristique de la ligne est Z^c = L¹/C¹. Une ligne de longueur quelconque peut être considérée comme une suite de tronçons courts placés bout à bout (fig. 5).

Influence des pertes dans une ligne de transmission

Si les conducteurs et les diélectriques d’une ligne ne sont pas parfaits, les résultats précédents cessent d’être valables. En fait, on s’arrange pour que les imperfections dues aux caractères imparfaits des matériaux restent faibles. La répartition des champs dans un plan de section droite ainsi que la vitesse de propagation ne sont pas affectées. Le seul phénomène nouveau est constitué par la diminution de l’amplitude de l’onde en fonction de la propagation le long de la ligne de transmission. Il en résulte une variation de la puissance transportée suivant la loi:

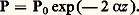L’atténuation de la ligne, caractérisée par le coefficient 見, est due à deux causes: l’effet Joule dans les conducteurs, les pertes diélectriques dans l’isolant.

Dans l’expression de l’impédance de ligne à faibles pertes, il convient de remplacer l’exponentielle exp(face=F0019 漣 jkz ) par exp(face=F0019 漣 見 + jk )z ; en introduisant, par ailleurs, le facteur de propagation complexe p = 漣 ( 見 + jk ), on obtient:

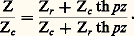3. Guides d’ondes U.H.F.

Depuis le début de la Seconde Guerre mondiale, les ondes ultra-courtes ont subi un développement accéléré grâce au radar puis aux faisceaux hertziens. Il n’est pas possible, pour des longueurs d’ondes centimétriques ou décimétriques, d’utiliser des lignes bifilaires classiques; on les a donc remplacées par la ligne coaxiale. Mais les pertes de transmission dans ce type de ligne proviennent essentiellement du conducteur central, d’où l’idée de le supprimer et de rendre inutile l’emploi de diélectrique intérieur. On ne conserve ainsi que le conducteur extérieur. Un tel tube est susceptible de transporter de l’énergie «hyperfréquence» pourvu que son diamètre soit de dimensions suffisantes. On constate également qu’il lui est possible de véhiculer entre l’émetteur et l’antenne des puissances de crête très élevées, par exemple plusieurs dizaines de mégawatts crête en bande S (3 000 MHz) avec pressurisation.

De nombreux types de guides d’ondes ont vu le jour, guides à sections rectangulaire, ronde, en U, en H, etc. Pratiquement, on en emploie deux aujourd’hui: les guides d’onde à section rectangulaire et ceux à sections ronde ou elliptique, utilisant le mode de propagation guidé TE 01.

Les guides sont obtenus par des procédés de mécanique classique: moulage, ou étirage, les assemblages étant réalisés par brasage; dans le cas de pièces en alliage léger, ce brasage est fait dans un bain de sels fondus à température assez élevée nécessitant un matériel spécial. Pour les ensembles U.H.F. délicats, difficilement réalisables par les procédés classiques d’usinage, on utilise l’électroformage (dépôt électrolytique en épaisseur sur un mandrin extrait ou dissous après formation du dépôt).

Le mode de propagation TE 01

Dans un guide rectangulaire métallique de section droite a 憐 b (la hauteur a est inférieure à la demi-largeur b /2), rempli d’un diélectrique de constantes 﨎猪 (habituellement de l’air), peut se propager une onde guidée TE 01 également appelée H 01. Le champ électrique est parallèle au côté a , le champ magnétique est situé dans le plan y Oz (fig. 6 a).

Si la fréquence utilisée possède dans le diélectrique indéfini la longueur d’onde, la propagation dans le guide a pour longueur d’onde^g définie par la relation:

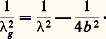Il existe ainsi une longueur d’onde de coupure^c = 2 b telle que, si 礪^c , la propagation se fait dans le guide sous forme de mode évanescent. Le guide se comporte donc comme un filtre de fréquence «passe haut».

Il est essentiel d’avoir une seule onde progressive et non pas un système d’ondes stationnaires. Pour cela, on sait réaliser des «terminaisons sans réflexion», appelées encore «charges adaptées» qui, placées en bout de guide, absorbent entièrement l’onde incidente sans donner lieu à une réflexion.

À l’aide des équations de Maxwell et des conditions aux limites, on peut trouver les équations du champ électromagnétique (les lignes de champs électrique et magnétique sont représentées figure 6 b):

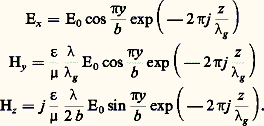La relation d’Ampère で^T = も^s 廬 ぴ permet de déduire les trois composantes du courant superficiel dans les parois du guide. On donne figure 6 c une représentation des lignes de courant sur deux faces du guide d’onde.

La notion d’impédance est peu utilisée pour les guides d’onde car elle n’est pas indépendante de la longueur d’onde employée. Néanmoins, pour une onde progressive, on peut définir l’impédance d’onde comme le rapport:

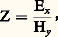qui est le même en tout point de l’onde. Pour un guide plein d’air, on trouve

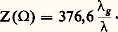En utilisant le flux du vecteur de Poynting («la puissance moyenne dissipée à l’intérieur d’une surface fermée est égale à la partie réelle du flux du vecteur de Poynting complexe à travers cette surface»), on calcule l’expression de la puissance moyenne transportée; pour une onde progressive dans un guide plein d’air, elle était:

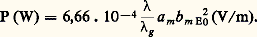L’atténuation dans un guide de cuivre rempli d’air est faible; pratiquement, elle est due uniquement aux pertes par effet Joule dans le conducteur métallique.

Autres modes de propagation dans un guide rectangulaire

La résolution des équations de Maxwell, dans le cas général de propagation sur guide rectangulaire de dimensions a 憐 b , montre qu’il est possible de propager des modes transversaux électriques du type TE^np (ou E^np ), et des modes transversaux magnétiques du type TM^np (ou M^np ), n et p étant des nombres entiers (p 0).

Ces deux types de modes possèdent également une longueur d’onde de coupure^c , donnée par l’expression:

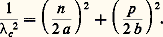Ces longueurs d’onde de coupure sont toujours inférieures à la longueur d’onde de coupure ^c01 du mode TE 01, celle immédiatement supérieure est^c02 correspondant au mode TE 02. Comme l’utilisateur ne cherche à faire propager dans un guide d’onde qu’un seul type de mode sans possibilité de transformation en un autre type, on comprend l’emploi pratiquement unique du mode TE 01 avec des longueurs d’onde comprises entre ^c01 = 2 b et ^c02 = b , soit dans un octave de fréquence.

Guides d’ondes circulaires

La résolution des équations de Maxwell en coordonnées cylindriques r , , z conduit à l’équation différentielle de Bessel. Désignons par 﨡^mn les zéros de la fonction de Bessel du premier ordre J^m (x ); à chaque valeur 﨡^mn correspond un mode de propagation TH^mn . Les modes de propagation TE^mn , quant à eux, correspondent aux zéros de la fonction de Bessel du second ordre J ^m (x ). La longueur d’onde de coupure est donnée par l’expression:

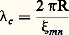(R, rayon du guide d’onde).

Le mode fondamental qui correspond à la longueur d’onde de coupure la plus grande est le mode de TE¹¹. En fait, il faut sans arrêt obliger la direction du plan de polarisation principale du champ électrique à ne pas tourner au cours de la propagation du mode TE¹¹.

Un autre mode de propagation, le mode TE⁰¹ est très utilisé en télécommunications. Malgré le très gros inconvénient de ne pas être le mode fondamental, il présente le gros avantage de véhiculer de l’énergie dans le domaine des hyperfréquences avec des pertes de plus en plus faibles à mesure que la fréquence augmente (fig. 7).

Guides d’ondes elliptiques

Les guides d’ondes elliptiques ont une section elliptique et véhiculent le mode guidé TE 01 comme mode fondamental. Si la longueur du petit axe de l’ellipse est égale au petit côté d’un guide rectangulaire et la longueur du grand axe de l’ellipse est égale au grand côté du guide rectangulaire, ces deux guides peuvent transporter des fréquences et des puissances semblables. Le périmètre de la section elliptique est alors plus petit que celui de la section rectangulaire; il est normal que les pertes par effet Joule dans les parois du guide elliptique soient plus faibles. Néanmoins, dans ce dernier, la bande passante du mode fondamental est plus étroite. En général, les guides elliptiques sont faits d’une faible épaisseur d’aluminium enrobée dans un plastique souple. On peut ainsi les enrouler et les fabriquer en grande longueur. Leur emploi dans des ensembles radars, où le cheminement entre émetteur et antenne est long et complexe, s’est généralisé.

4. Lignes U.H.F. à mode de propagation TEM

Le câble coaxial

Une ligne coaxiale est constituée par deux conducteurs cylindriques de révolution autour du même axe (fig. 8). Le conducteur central est maintenu par des rondelles isolantes ou par un diélectrique plein.

En propagation TEM, les champs électrique et magnétique au point M sont dans le plan de la section droite. Le champ électrique se déduit immédiatement du champ électrostatique; il est radial et de la forme:

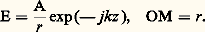Le champ magnétique s’exprime:

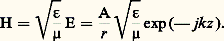Le courant dans le conducteur central se calcule à partir du théorème d’Ampère:

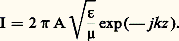L’impédance caractéristique Z^c se déduit des expressions de la tension et du courant. La tension V entre les conducteurs étant:

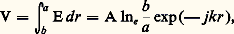elle vaut:

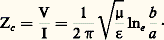Si l’isolant est l’air:

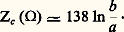En ce qui concerne les éléments du schéma équivalent d’une ligne coaxiale supposée sans perte, la self-inductance par unité de longueur est:

la capacité par unité de longueur est: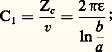

la puissance maximale transportable est:

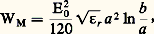E⁰ étant la rigidité diélectrique de l’isolant utilisé.

Tout comme pour le guide d’onde, les équations de Maxwell montrent qu’il est possible de propager dans une ligne coaxiale des modes TE^np et TM^np . Chacun de ces modes possède une longueur d’onde de coupure au-dessus de laquelle le mode devient évanescent. Pour éviter un mélange de modes toujours désastreux pour l’utilisateur, on n’emploie pratiquement pas les modes TE^np et TM^np . Le mode TEM qui ne possède pas de longueur d’onde de coupure est en général le seul utilisé.

Lignes triplaques (stripline)

La configuration d’une ligne triplaque peut être considérée comme la phase finale d’une déformation progressive par écrasement d’une ligne coaxiale (fig. 9).

Le conducteur central devient un ruban plat de faible épaisseur; le conducteur extérieur est «cassé» en deux plans appelés «plans de terre». Le mode de propagation fondamental est le mode TEM. Les notions de champ électromagnétique, courant, tension, impédance, puissance transportée se déduisent de celles de la ligne coaxiale.

De sa commodité d’emploi (conducteurs plans faciles à usiner et à modifier pour créer des éléments hyperfréquences à large bande d’accord) provient tout l’intérêt de la ligne triplaque, très utilisée en basse puissance (coupleurs directifs, détecteurs, circulateurs à ferrite, etc.).

Ligne à ruban ou microstrip

La ligne de transmission microstrip se compose d’un ruban métallique déposé sur une face d’une plaquette de diélectrique, l’autre face étant entièrement métallisée et servant de plan de masse. Le diélectrique le plus utilisé est l’alumine ( 﨎^r 黎 10) et plus rarement le ferrite ( 﨎^r 黎 15). Ce type de ligne de transmission comporte plusieurs avantages: d’abord, son élaboration technologique est relativement simple et permet une bonne reproductibilité, même dans le cas où le circuit de propagation comporte des éléments hyperfréquences compliqués; ensuite, sa structure est du type «planar», c’est-à-dire que les divers éléments constitutifs sont d’accès facile; la mécanique d’assemblage réduite au minimum est favorable à la soudure par thermo-compression qui permet d’adjoindre divers éléments semi-conducteurs directement déposés sur la ligne; enfin, l’emploi de diélectrique à constante 﨎^r relativement élevée permet une bonne concentration de l’énergie et la réduction des dimensions.

La théorie des lignes microstrip proposée par H. A. Wheeler (1964) est celle qui permet la meilleure interprétation des résultats expérimentaux: il n’existe pas de solution exacte des équations de Maxwell et le calcul approché de Wheeler est fondé sur les transformations conformes. La difficulté essentielle réside dans la discontinuité du milieu de propagation qui oblige à tenir compte de la déformation des lignes de champs électromagnétiques. Cependant, l’hypothèse fondamentale reste que le mode de propagation est le mode TEM.

La technologie des lignes triplaques et microstrip est traitée dans l’article MICROÉLECTRONIQUE.

5. Transmission par fibres optiques

Principe

Dès l’Antiquité, les Grecs connaissaient le phénomène de propagation de la lumière dans des cylindres transparents. Au XVI^e siècle, ce phénomène était utilisé dans des fontaines lumineuses; mais ce n’est réellement que pendant la seconde moitié du XX^e siècle que l’intérêt et le développement industriel des fibres optiques sont apparus. Cela s’est matérialisé en France par la mise en service, en 1980, de la liaison des deux centraux téléphoniques parisiens Tuileries et Philippe-Auguste, à l’aide d’un câble comprenant soixante-dix fibres optiques.

La fibre optique la plus simple consiste en deux cylindres concentriques de matériaux diélectriques d’indices de réfraction différents. Le cœur (fig. 10) d’indice n ¹ est placé au centre d’une gaine optique d’indice n ² (n ² 麗 n ¹) appelée «manteau» (cladding ) pour la distinguer de la gaine de protection mécanique extérieure.

Les lois de Descartes relatives à la propagation d’une onde lumineuse entre deux milieux d’indices différents s’appliquent et les rayons lumineux introduits dans le cœur sont guidés par ce dernier si l’angle d’incidence à l’interface cœur-gaine optique est supérieur à l’angle limite ^L, défini par sin ^L = n ²/n ¹ (fig. 11). Pour réaliser cette condition, il est nécessaire que l’angle I du faisceau pénétrant dans la fibre, par rapport à l’axe de la fibre, soit inférieur à un angle limite I^L défini par sinI^L = 連n ¹² 漣 n ²². I^L est appelé «ouverture numérique» de la fibre.

En fait, la propagation des ondes à l’intérieur de la fibre n’est pas uniquement limitée au respect de la condition 礪 ^L à l’interface cœur-gaine optique. Une infinité de rayons lumineux peut se propager dans le cœur de la fibre en respectant cette condition; ils peuvent se superposer en phase, ou se détruire en opposition de phase (problème des interférences). Ainsi, les angles d’ouverture I susceptibles de favoriser la propagation avec de faibles pertes à l’intérieur du cœur ne prennent pas toutes les valeurs comprises entre 0 et I^L, mais un certain nombre de valeurs discrètes, qui correspondent à des modes de propagation guidée avec des pertes minimales.

Le type de fibre qui vient d’être décrit, appelé à «saut d’indice», possède une variante intéressante, les fibres à «gradient d’indice». On rend les trajets optiques des différents rayons à l’intérieur du cœur pratiquement identiques, en faisant varier l’indice de réfraction en fonction de la distance radiale, suivant une loi pratiquement parabolique (fig. 12 a). La gaine optique peut disparaître, et les rayons lumineux correspondant aux différents modes de propagation à faible perte sont continûment déviés par la variation radiale de l’indice; ils ne subissent pas de réflexion totale à la limite du cœur de la fibre (fig. 12 b).

Propagation et modes dans une fibre optique

Les modes de propagation à l’intérieur d’un cylindre diélectrique à section circulaire sont bien connus. Ils sont de manipulation compliquée, mais on possède des solutions numériques pour les valeurs propres. Cependant, ces dernières peuvent prendre des expressions asymptotiques précises et plus simples lorsque:

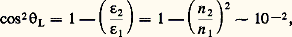où 﨎¹, 﨎², n ¹, n ² sont les constantes diélectriques et les indices de réfraction du cylindre et du milieu extérieur.

Dans le cas d’une fibre à saut d’indice , ( 﨎¹, n ¹) correspond au cœur et ( 﨎², n ²) à la gaine optique; 1 漣 ( 﨎²/ 﨎¹) peut être voisin de 0,5, mais on démontre que les expressions asymptotiques sont encore valables à 10 p. 100 près.

L’étude de l’excitation et de la dispersion des modes dans une fibre optique permet de déterminer l’aptitude de cette fibre à supporter des modes de propagation à faible perte. La dispersion est donnée par l’expression:

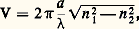où a est le rayon de la fibre et, la longueur d’onde de la radiation lumineuse. On démontre que le nombre total de modes pouvant être transportés par la fibre est:

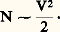Il est possible de concevoir une fibre optique où ne se propage qu’un seul mode guidé avec une polarisation déterminée; cela est obtenu pour V 麗 2,404 8; il faut à la fois un diamètre du cœur faible (face=F0019 黎 5 猪m) et une différence d’indice n = n ¹ 漣 n ² 黎 10^-2.

Dans une fibre à gradient d’indice , l’étude complète de ces modes de propagation a mis en évidence de façon statistique l’importance de conserver le profil d’indice de la section sur toute la longueur de la fibre, ainsi que l’influence de défauts de la fibre et de son conditionnement.

Ce type de fibre propage un nombre de modes discrets donné par:

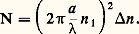Ici également, avec a et n faibles, on peut obtenir une propagation monomode. Il est intéressant de noter que, à diamètre et différence d’indice identiques, une fibre à gradient d’indice propage deux fois moins de modes qu’une fibre à saut d’indice.

Débit théorique d’information

Le débit d’information d’un guide d’onde diélectrique uniforme est limité par trois paramètres: d’abord, la dispersion du matériau en fonction de la longueur d’onde; ensuite, la dispersion du guide d’onde (c’est-à-dire que pour un mode donné la vitesse de propagation, ou nombre d’onde, varie en fonction de la longueur d’onde); enfin, la variation de la vitesse de groupe, si plusieurs modes se propagent à une fréquence donnée.

Le débit des fibres monomodes ne prend en compte que les deux premiers phénomènes. Son calcul théorique se fait en introduisant à l’entrée de la fibre un train d’impulsions de forme gaussienne normalisée (fig. 13):

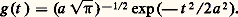On montre par le calcul qu’à la sortie de la fibre, le train d’impulsions est composé d’impulsions élargies; l’élargissement dépend de la longueur L de la fibre, du coefficient d’absorption et de h , dérivée seconde par rapport à la fréquence, du nombre d’onde. Puis intervient le paramètre 嗀, qui est la fraction maximale d’intensité tolérée de recouvrement entre deux impulsions successives en sortie. On déduit alors le débit maximal correspondant:

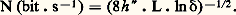À titre indicatif, la figure 14 représente la variation de N en fonction de la longueur d’onde pour différents couples de valeurs (L, ), où L est exprimée en kilomètres et = 漣 10 lg 嗀. On remarque que pour = 1,3 猪m, la bande passante devient théoriquement infinie, car la dispersion du guide d’onde annule la dispersion du matériau.

Pratiquement, la bande passante des fibres monomodes est de 10 Gbit 練 s^-1 練 km^-1 environ.

Pour les fibres multimodes, la limitation du débit provient essentiellement du fait que chaque mode se propage avec une vitesse de groupe différente. Pour une fibre à saut d’indice, une impulsion brève à l’entrée se distribue dans plusieurs modes guidés; on obtient en sortie un train d’impulsions dans un intervalle de temps:

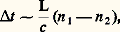où c est la vitesse de la lumière.

Si l’on considère que la période d’information est 2 t , le débit d’information se restreint à 10 Mbit 練 s^-1 練 km^-1 environ.

La faculté de transmettre des informations pour les fibres multimodes à gradient d’indice est plus élevée; en effet, l’élargissement t à la sortie de la fibre d’une impulsion brève est:

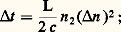dans les mêmes conditions que ci-dessus, le débit d’information atteint alors quelques gigabits par seconde et par kilomètre.

On trouvera dans l’article TÉLÉCOMMUNICATIONS - Télécommunications optiques des informations pratiques sur la technologie et les caractéristiques des fibres optiques modernes.

Encyclopédie Universelle. 2012.